俄罗斯总理的几何题
9 月 1 日是俄罗斯的知识节,因为这一天是各级学校的开学日,象征进入知识宝库的日子。
今年的知识节,俄罗斯总理米哈伊尔·米舒斯京(Mikhail Mishustin)来到莫斯科物理技术学院(MIPT)视察。该校是俄罗斯顶级的理工科大学,出过许多诺贝尔奖得主和著名科学家。

米舒斯京总理来到新生的教室,给学生们讲话。他看到黑板上写满了数学公式,一时兴起,就上前写了一道数学题,要求大家当场解答。

根据维基百科,米舒斯京生于 1966 年,大学专业是系统工程,主修计算机辅助设计。工作以后,还读过一个经济学博士。在担任总理之前,他是俄罗斯联邦税务局长。

他出的是一道几何题,题目如下。
给定圆上的一个点和一条直径,你能否找到一种方法,画出从该点到直径的垂直线(下图的绿线)。
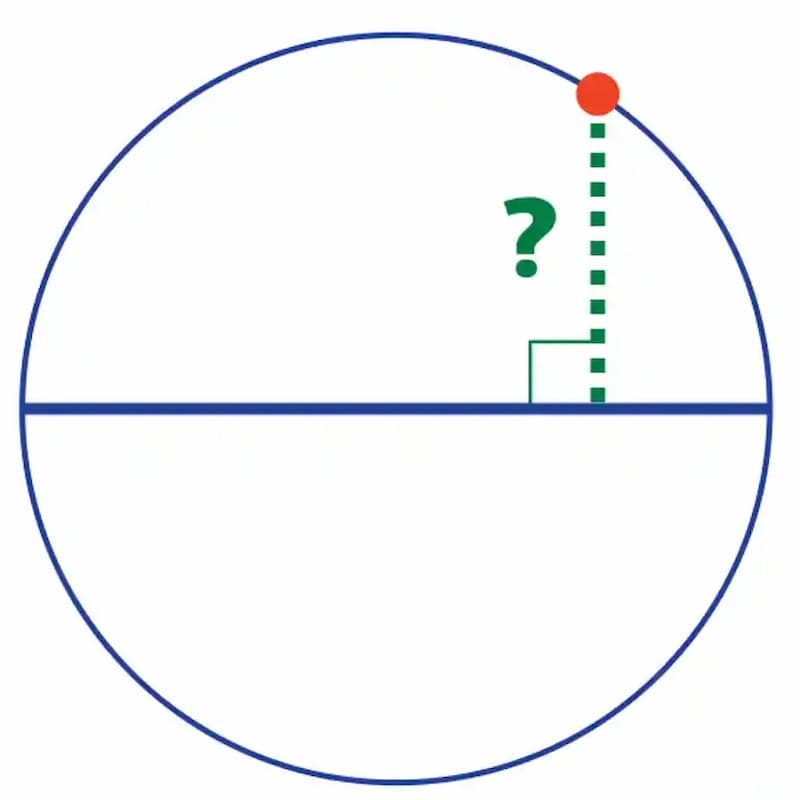
这道题的难点在于,你不能使用任何测量工具,唯一可以用的就是一把不带有标记的直尺。
大家可以思考一下,这道题怎么解。
虽然它用不到高深的数学知识,初中的几何学课程就可以解答,但也不算容易。你必须知道两个基本的几何定理,才能想出答案。
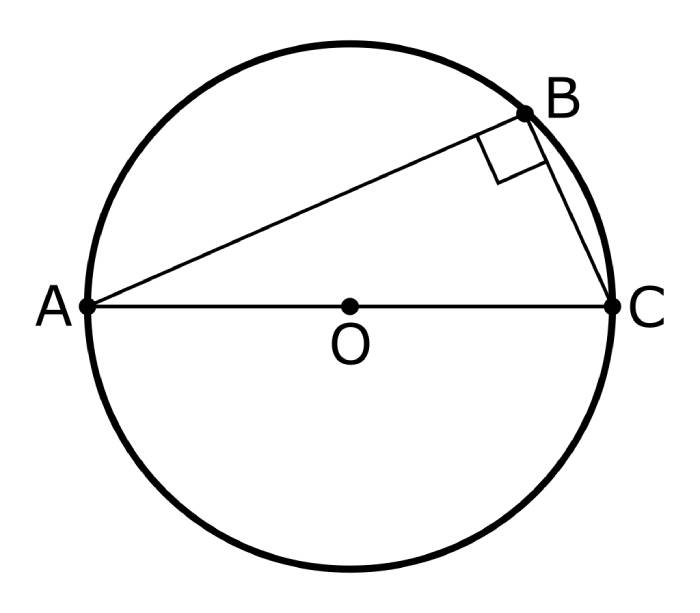
第一个是泰勒斯定理,欧几里得《几何原本》提到过: 圆上任意一点与直径组成的三角形,是直角三角形。
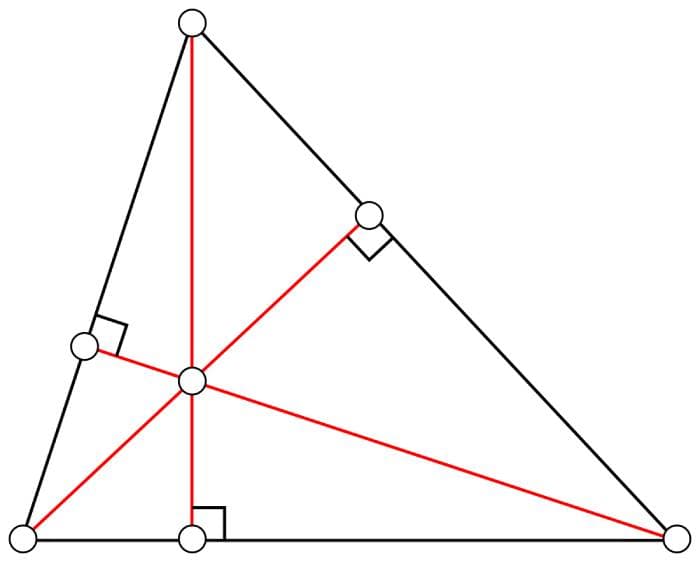
第二个定理是: 锐角三角形的三条高交于一点。
如果你已经忘了这两个定理,可以再去看一下初中几何课本,这里就不给出证明了。
下面我根据一个数学家写给英国《卫报》的文章,介绍如何解答这道题。
如果你还想再思考一下,自己找到答案,那就暂时不要往下看了。我要讲答案了。
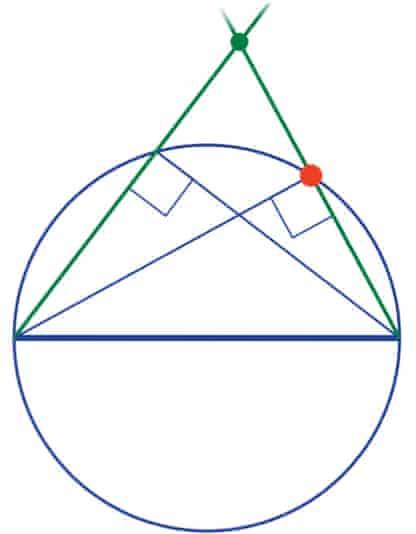
第一步,在相同的半圆上,任意再找一个点。将这两个点,与直径的相邻端点连起来,连线延长后可以形成一个三角形。
上图中,圆周上的两个点与直径组成的,都是直角三角形。它们可以看作直径的两个端点到绿边的两条高。
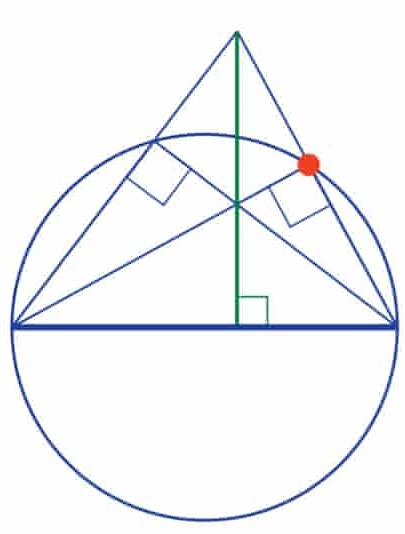
第二步,上一步的两条高产生了一个交点,将这个交点与三角形的外部顶点连起来,延长后与直径相交。
根据三角形的三条高交于一点,可以知道,上图的绿线是直径的一条垂直线。后面只需要找到它的平行线,穿过红点即可。
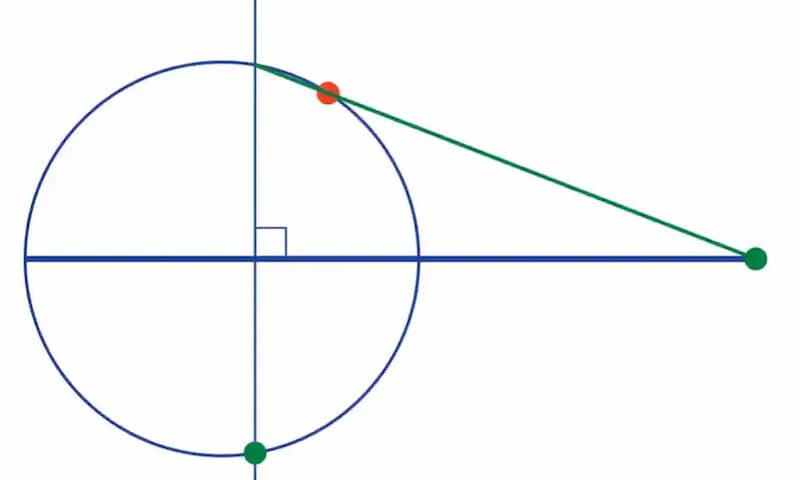
第三步,上一步的绿线与圆周有一个交点,将这个交点与红点连起来,延长后与直径相交(上图的第一个绿点)。
同时,将上一步的垂直线延长,与另一侧的圆周相交,产生一个交点(上图的第二个绿点)。
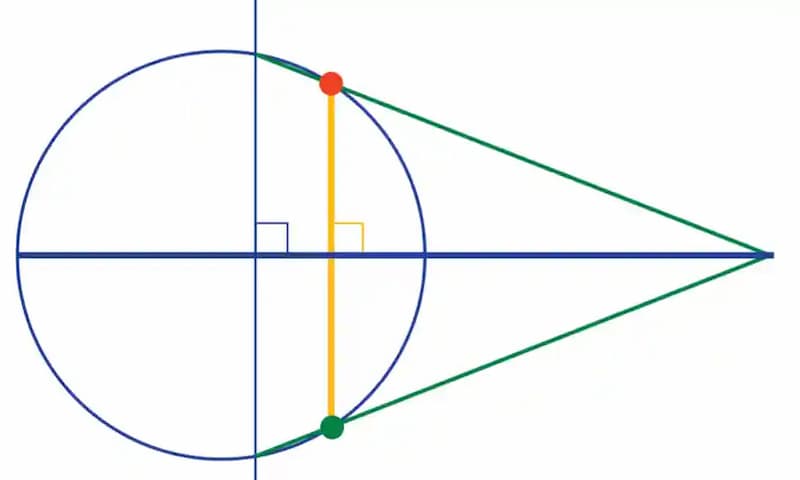
第四步,将上一步的两个绿点连起来,这条线会与圆周产生一个交点(上图的绿点)。
再将绿点与红点连起来(上图的黄线),这就是我们所要寻找的答案:红点到直径的垂直线。
这是因为上图的两条绿边与第二步的垂直线,形成了一个等腰三角形,原始的那条直径就是等腰三角形顶点到底边的高。这意味着,红点与绿点是对称的,它们的连线平行于底边,所以垂直于高(直径)。
至此,整道题解答完毕。


米舒斯京总理在黑板上画完解题过程后,对学生们说:
“你们会在大学里面,学到数学、物理、化学知识,但是不要忘了那些基础知识。基础知识与专业知识结合起来,你就能解决任何问题,不仅是科学问题,也包括商业问题。”



